Here’s a question for everyone who does numerical computation. Has anyone released an open-source 1-d interpolation algorithm with assembly code for the various kinds of processor SIMD extensions (i.e. SSE2, 3DNow, AltiVec)?
Most (if not all) scientific codes make repeated use of expensive numerical functions, and a quick glance through a few scientific codes (including my own) have convinced me that a fast interpolation scheme (particularly of sqrt() ) would speed up most scientific codes by factors of 2 or more. A typical Molecular Dynamics code will calculate square roots and functions like the Lennard-Jones potential,
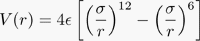
or the Buckingham potential,
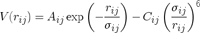
billions of times per timestep. Sqrt and exp (and the LJ and Buckingham potentials) are smooth, and we typically only need functions like this computed over a relatively short range of values. Cubic splines give you twice differentiable approximations, and precomputing the functions you need on a 1-d grid is trivial.
There are plenty of open-source cubic spline codes out there (i.e.PSPLINE, SPLINE, Carl De Boor’s Practical Guide to Splines fortran code, and many more). None of these codes (at least none of the ones I’ve seen) take advantage of the streaming multimedia extensions (SSE2, 3DNow, AltiVec) on modern processors. We hear great things about how fast these extensions are for Non-Uniform Rational B-Splines (NURBS), and for color interpolation in 2-d, but the demonstration assembly-language codes are pretty far beyond what most physicists, chemists, or biologists could easily splice into their programs.
What would really give scientific codes a boost, would be a fortran- or c-callable routine that let the user store an array of x and y values, and then branched to assembly language for the lookup of interpolated values.
Am I missing some code that anyone else knows about?
[tags]splines, simd, open source, scientific computing[/tags]
I suspect you may indeed be missing something, due to looking in the wrong place — specifically, due to looking for “SIMD” in the source code of the interpolators, rather than looking for it in compiler optimizations.
I’d think it would be fairly easy to write a spline code such that a compiler’s vectorizer would pick up on the main loop, and it’s simple enough that even a relatively unsophisticated vectorizer ought to do a reasonable job of it. Intel’s compiler, at least, has switches to write SIMD code for auto-vectorized loops if one uses the right compile-time switches; I suspect that GCC either has the same or will have it soon, but I don’t have the relevant documentation handy.
Also, doing it directly in the source code doesn’t necessarily require assembly-coding; while trying briefly and unsuccessfully to figure out the current state of SIMD support in GCC’s vectorizer, I came across this tutorial on using GCC compiler builtins for SIMD instructions in C code.
Also, do you know that the arithmetic is actually the bottleneck in a spline interpolation? A quick look at the SPLINE library you mentioned gives me the impression that the process of searching for the bounding interval was likely to take up at least as much time — unless the points are equally spaced, which SPLINE doesn’t implement, that’s O(log n) for n interpolation values at best, whereas the actual interpolation is O(1). It’s almost certainly worth doing some code profiling before trying to do the optimization!
On a completely different note, I should point out that one of the GCC SSE builtins is a square-root calculation. For that, there’s almost certainly no point at all in writing your own function based on a general-purpose interpolator (no matter how good), as the GCC one most likely does it better with a special-purpose routine. For that matter, it may be worth cribbing GCC’s routine for that to use as an interpolator for other functions.
That’s a good point about the square root optimizations. We discovered that for ourselves last week while coding up this module. The compiler- or hardware-supplied square roots are pretty darned fast. None of the splines we attempted could get any faster (and we usually lost performance).
We also rewrote some of the standard interpolation codes to have two interaces to the lookup of the y value. One, called lookupUniformSpline, will assume you have a uniform grid. Like you mentioned above, if you have to search for the interval (i.e. if you have x-values that are non-uniform), you don’t get much of a speedup over doing the raw math of the function iteself unless your function is really expensive.
One nice feature is that the new interpolation makes a screened coulomb interaction like (q_i q_j erfc(a r)/r) into essentially the same cost as the bare coulomb interaction, and it brought down the cost of the (a/r)**m interactions in the Sutton-Chen force field by 50%.
I think that is a great idea. The price of using interpolated results would be a numerical difference at each step, however small it is, as opposed to directly using the system’s routines to compute analytical expressions. I initially thought that this might cause the potential to be effectively different from the original analytical one, say, Lennard-Jones. But then I realized that no numerical solution is perfectly analytical. So there should not be any problem of using this. No doubt that the total energy would be conserved, provided that the potential is calculated using the same interpolation method.
If someone can do a benchmark to see how fast it can be, it would be great. (Perhaps I will think about implementing this in my own code, as speed is our paramount consideration.)
Dan: Sounds good to me! It would be interesting to try writing a version of your lookupUniformSpline code that takes an array of x-values and loops over them in a loop that’s written tightly around the spline interpolation, to see if compiler parallelization speeds it up any.
Charles: The system routines are probably using a spline interpolation or a series approximation, anyway — few analytical expressions can be evaluated exactly via elementary operations. The trick, though, is that to get a “numerically perfect” answer, you merely need to have enough interpolation points or enough series terms that the error is too small to affect the least-significant bit of the result. With a reasonably high-order method and a nicely-behaved function, that’s not too difficult.
One other thing that occurs to me with this (though it’s probably obvious): Depending on how the code is structured, you ought to be able to get away with never calculating the distance itself at all. Write all the potentials in terms of the distance squared (which doesn’t require a square root to calculate), and interpolate that function instead.
If the potential energy were all that was required, a potential based on the distance squared would work. However, we also need forces, and the chain rule requires the value of r itself:
dV/dx = dV/dr * dr/dx = dV/dr * (x/r)
I haven’t yet figured out how to do forces splined on the value of r^2. We’d still need r values for the (x/r).
Let’s see:
dV/dx = dV/d(r^2) * d(r^2)/dx = dV/d(r^2) * 2x
So I’d need to spline V as a function of r^2 and then lookup the function and the first derivative. Looks like I have a new task for the afternoon….
Hey, that worked out remarkably well! I’d completely forgotten about the need for the force components (otherwise it would be a matter just of splining dV/dr as a function of r^2), so I’m pleasantly surprised at how neatly it turned out once those were included.