This news comes by way of John Parkhill, my new colleague here at Notre Dame.
This news comes by way of John Parkhill, my new colleague here at Notre Dame.
William G. Hoover (of the Nosé-Hoover Thermostat) and Carol G. Hoover issued a $500 challenge on arXiv to generate a time-reversible random number generator. The challenge itself would be quite remarkable news. What’s even better is that the challenge (including the source code for an implementation) was solved in 6 days by Frederico Ricci-Tersenghi.
Why is this a big deal? Most of the equations in physics that govern time evolution of particles obey time-reversal symmetry; the same differential equations that govern molecular or planetary motion will take you back to your starting point if you suddenly reverse the time variable. This is a usually a fantastic way to check to see if you are doing the physics correctly in your simulations, and also means that collections of starting points that are related to each other behave in certain predictable ways when they evolve.
Stochastic approaches to physical motion introduce an aspect of randomness to mimic the behavior of complex phenomena like the motion of solvent surrounding the molecule we’re interested in, or to mimic the transitions between different electronic states of a molecule. The introduction of random numbers has meant we had to give up time-reversibility, and we’ve been willing to live with that for a long time because we can study more complicated phenomena.
If we have access to a time-reversible pseudo-random number generator, however, we get that very powerful tool back in our toolbox.
Now, the Langevin equation,
\(m \frac{d^2 x}{dt^2} = F – \gamma(t) \frac{dx}{dt} + R(t)\)
has two things that prevent it from being time-reversible. Besides the stochastic or random force, \(R(t)\), there’s also a drag or friction force, \(-\gamma(t) \frac{dx}{dt}\), that depends on the velocities of the particles. There’s no solution yet to time reversibility for this piece (and I have my doubts that there ever will be a way to reverse this). I suppose if we offer up another $500 prize for time-reversible drag, we’d make some traction on this problem…
(The comic above courtesy of xkcd).
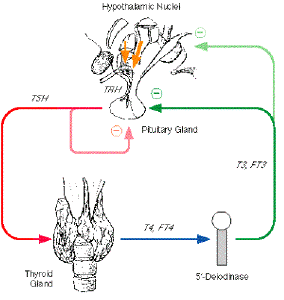 This is a bit outside our normal area of expertise, but it looks interesting.
This is a bit outside our normal area of expertise, but it looks interesting.
 Yesterday’s
Yesterday’s  This news comes by way of John Parkhill, my new colleague here at Notre Dame.
This news comes by way of John Parkhill, my new colleague here at Notre Dame.
 March 14th is \(\pi\)-day in the US (and perhaps \(4.\overline{666}\) day in Europe). The idea of a day devoted to celebrating an important irrational number is wonderful — I’d love to see schools celebrate
March 14th is \(\pi\)-day in the US (and perhaps \(4.\overline{666}\) day in Europe). The idea of a day devoted to celebrating an important irrational number is wonderful — I’d love to see schools celebrate