So our latest little obsession in research-land is something called The Jarzynski Equality, which is a strong statement about equilibrium thermodynamical quantities being exactly derivable from irreversible (non-equilibrium) trajectories. Jarzynski has a brief commentary in PNAS that describes it, but the major result is this equation:
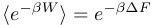
Here β is the inverse temperature (1/(kb T)), W is the work done to drive a system between two thermodynamic states, and ΔF is the free energy difference between these two states. The angle brackets around the left side stand for the average (performed over many repeated trials) of what’s inside the brackets.
Traditional thermodynamics tells us this:
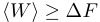 .
.The huge difference is that the traditional thermodynamic approach tells us that the work done to drive the system from one state to another is always greater than or equal to the difference in free energy between the two states. The conventional wisdom is that the equality is reserved for a special kind of driving that is done infinitely slowly (i.e. in thermodynamic terms, the system is driven reversibly). For any other kind of transformation (i.e. for any experiment that we can do realistically), the work done to drive the system should always be greater than the free energy difference.
Jarzynski’s equality says something much stronger. It says that we can get the free energy difference between two states by averaging a large number of irreversible experiments, and that our free energy estimates won’t be an upper bound, they’ll be the actual free energy difference.
If Jarzynski’s inequality is correct, this is a huge change in our understanding of how we use thermodynamics. It has, unsurprisingly, generated a lot of activity in the literature. Here’s a brief roadmap of what we’ve been reading on the subject:
Jarzynski first published this work in Phys. Rev. Lett. 78, 2690-2693 (1997) and elaborated a master equation approach in Phys. Rev. E 56, 5018-5035 (1997). Gavin Crooks Crooks tackled the equality using path-ensemble averages (Phys. Rev. E 61 2361-2366 (2000)). The best basic description of Jarzynski’s Equality we’ve found is in a wonderful article by Gerhard Hummer and Attila Szabo that relates the Equality to concepts like atomic force microscopy and steered molecular dynamics. Hummer & Szabo published their article in PNAS 98, 3658-3661 (2001).
There have been some sceptical papers in the literature. Cohen and Mauzerall puslished a paper in J. Stat. Mech. which was critical of the proof of the equality. Jaeyoung Sung has a paper up at arXiv that places some limits on the driving process.
There have also been attempts to add quantum mechanics to the picture, notably by Satoshi Yukawa and Shaul Mukamel.
From my perspective, this is all extremely exciting. We’ve got some non-equilibrium driving code that we use to drag molecules around to set up initial conditions for equilibrium simulations. It would be very nice if we could use that driving code to calculate free energy surfaces directly.
[tags]thermodynamics, statistical mechanics, molecular dynamics[/tags]